Search Results
36 results found with an empty search
- Do Wave Functions Vanish at Infinity?
Episode 5 of Quantum on the Back of an Envelope. In this episode of Quantum on the Back of an Envelope , In this episode of Quantum on the Back of an Envelope, we ask whether a quantum mechanical wave function really has to vanish at infinity — an assumption often made in introductory textbooks and courses. To explore this, we examine a specific example (taken from "Principles of Advanced Mathematical Physics" by Robert D. Richtmyer) of a wave function that is perfectly continuous, differentiable, and normalizable, yet not only refuses to vanish, but actually becomes unbounded at infinity.
- Quantum Zeno Effect
Episode 4 of Quantum on the Back of an Envelope. In this episode of Quantum on the Back of an Envelope , we explore how frequent observations -- more precisely, projective measurements -- can dramatically alter the time evolution of a quantum system, and in some cases even freeze it altogether. This fascinating phenomenon is known as the quantum Zeno effect.
- Quantum Fractals
Episode 3 of Quantum on the Back of an Envelope. In this episode of Quantum on the Back of an Envelope , we explore quantum fractals through one of the simplest quantum-mechanical systems: the particle in a box. The fractal wave function discussed here is based on the paper: M. V. Berry, Quantum fractals in boxes , J. Phys. A: Math. Gen. 29, 6617 (1996) .
- Attractive Potential with No Ground State
Episode 2 of Quantum on the Back of an Envelope. In this episode of Quantum on the Back of an Envelope , we explore the strange and fascinating -1/x ² potential. Despite being attractive and infinitely deep, it has no ground state -- and therefore no discrete energy spectrum. In a certain regime, the system can be so unstable that it could (theoretically) destroy the universe. No equations -- just simple dimensional analysis.
- Spontaneous Singularities
Episode 1 of Quantum on the Back of an Envelope. In this first episode of Quantum on the Back of an Envelope , we explore an unexpected phenomenon in quantum mechanics: how a perfectly smooth wave function, evolving under the Schrödinger equation, can spontaneously develop a singularity over time.
- H₂⁺ Molecular Ion in a Box
This is a two-dimensional model of the simplest molecular ion, consisting of two protons and one electron. The electron, represented by a red-yellow probability wave, interacts with each proton, shown as blue dots, through a nonsingular Coulomb potential, defined as V(r) = -1/(r + ε). The system is confined within a box with perfectly reflecting walls (grey square). The cyan curve represents the mean position of the electron. The time evolution of the electron's probability density has been computed by numerically solving the time-dependent Schrödinger equation.
- Calculus Refresher: Question 12
Calculate the following integral: Solution:
- Calculus Refresher: Question 11
Calculate the following limit. Here is the solution.
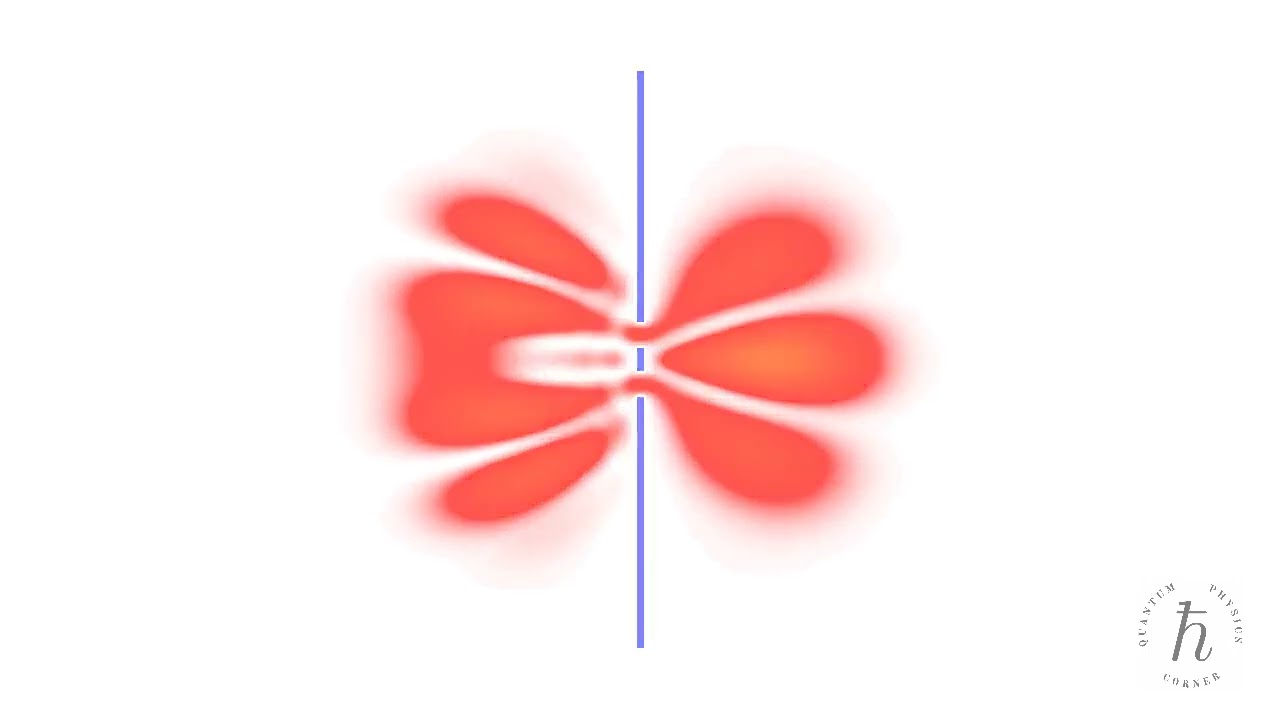
- Double-slit interference
A quantum particle passes through an opaque screen with two slits, resulting in an interference pattern. The time evolution of the probability density is determined by numerically solving the time-dependent Schrödinger equation.
- Calculus Refresher: Question 10
Find the following integral. Here are two solutions.